9663번: N-Queen

nolbo
2025-3-7
난이도
골드 IV
알고리즘 분류
#백트래킹backtracking#브루트포스 알고리즘bruteforcing

분석

유명한 N-Queen 문제이다. N x N 체스판에 퀸 N개를 서로의 공격 범위에 들지 않게 배치하는 경우의 수를 구해야 한다.

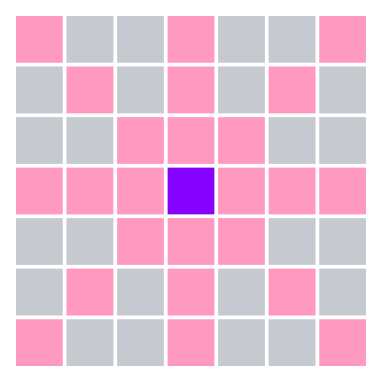
퀸의 공격 범위는 자신이 위치한 행과 열, 그리고 자신을 중심으로 하는 대각선이다. 아래의 이미지에서 보라색 칸은 퀸의 위치, 빨간색 칸은 퀸의 공격 범위이다.

4 x 4 체스판을 사용한 예를 보자. 아래 이미지와 같이 1행 1열에 퀸을 둠으로써 시작한다.

2열에 퀸을 놓을 수 있는 칸은 3행과 4행이다. 우선 3행에 퀸을 놓아보자.

3열에 퀸을 놓을 수 있는 자리가 존재하지 않게 된다. 그러므로 1행 1열, 3행 2열에 퀸을 놓으면 4 Queens를 만족할 수 없게 된다. 이를 반복하다보면 4개의 퀸을 배치한 경우를 발견할 수 있다.

이번 문제의 목표는 N Queen 문제를 알고리즘으로 빠르고 쉽게 풀어내는 것이다. 해당 문제를 푸는 대표적인 방법은 2가지, 브루트포스 알고리즘과 백트래킹이다.

브루트포스 알고리즘

브루트포스 알고리즘(brute force algorithm)의 다른 이름은 '무차별 대입'이다. 즉, 경우의 수 하나하나 모두 대입해보는 알고리즘이다.

브루트포스 알고리즘이 유용한 문제도 존재하겠지만, 적어도 이 문제는 아니다. N Queen을 브루트포스로 풀 경우 O(NN)O\left(N^{N}\right)이라는 놀라운 시간복잡도를 갖게 될 것이다.

백트래킹

백트래킹(backtracking)은 탐색 알고리즘에 퇴각 메커니즘을 대입한 형태이다. 경우의 수를 탐색 도중 해당 경우의 수가 목표를 달성하지 못하리라 판단되면 탐색을 멈추고 이전 탐색 과정으로 돌아가 다른 경우의 수를 시도한다.

어떤 알고리즘인지만 들어도 브루트포스보다 더 나을 것 같은 느낌이 든다. 실제로 N Queen을 백트래킹으로 풀 경우 O(N!)O\left(N!\right)의 시간복잡도를 갖게 될 것이다. 이 글에서는 백트래킹을 사용해 문제를 풀 것이다.

답안

#include <iostream>

using namespace std;

int r = 0;

void nQueen(int n, int depth, int* queen) {
    if (n == depth) {
        r++;
        return;
    }

    for (int i = 0; i < n; i++) { // depth열의 공간 순회
        bool enable = true; // i행 depth열에 배치 가능 여부

        for (int j = 0; j < depth; j++) { // queen 배열 순회
            if (i == queen[j] || (abs(i - queen[j]) == abs(depth - j))) { // 같은 행에 있거나 || 대각선 범위에 포함될 경우
                enable = false;
                break;
            }
        }

        if (!enable) continue;

        queen[depth] = i;
        nQueen(n, depth + 1, queen);
        queen[depth] = 0;
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n;
    cin >> n;

    nQueen(n, 0, new int[n]());
    cout << r << '\n';
}

풀이

해당 답안에서는 탐색 알고리즘으로 깊이 우선 탐색(DFS)을 채택했다. 위 코드에서 설명할 만한 부분은 퀸의 배치 현황을 저장할 데이터가 2차원 배열이 아닌 1차원 배열이라는 점이다.

보통 2차원 배열을 사용하는 이유는 퀸이 놓인 위치의 행과 열을 저장하거나, 체스판 전체를 2차원 배열화하기 위해서이다. 그런데, 꼭 그렇게 해야만 할까?

N Queen을 만족하기 위해선 하나의 열, 하나의 행에 존재하는 퀸은 유일해야 한다. 어차피 이 조건을 만족하지 않으면 N Queen에 도달할 수 없다. 그러므로 퀸은 무조건 하나의 열에 하나만 존재한다고 간주하고 열의 정보는 배열의 인덱스를 활용하면 1차원 배열(queen 배열)로 문제를 풀 수 있다.

그러면 1차원 배열을 사용했을 때 대각선 범위의 판정은 어떻게 해야 할까?

#lightonly
#darkonly

보라색 칸은 이미 놓인 퀸의 위치, 파란색 칸은 새로 놓으려는 퀸의 위치이다. 파란색 칸은 퀸의 대각선 공격 범위에 포함되므로 놓을 수 없다. 이를 판단하는 방법은 이미 놓인 퀸과 놓으려는 퀸 사이의 거리이다. 대각선 공격 범위에 포함될 경우, 퀸과의 가로 거리와 세로 거리가 같음을 이용하면 대각선 범위를 고려하기 위해 반복문을 사용하지 않아도 된다.